
In a recent visit to a local museum in my home town, two actors re-enacted an exchange between Albert Einstein and the local scientist Hendrik Lorentz, both Nobel Prize laureates (seated next to one another in the famous Solvay conference picture).

Einstein had discovered that measurements on the positions of stars were biased. The reason is, he argued, that the light emitted from these stars was subject to gravitational pull from, for example, the sun. The light would therefore bend slightly before arriving at the earth. Unaware of such bending, scientists at the time believed that their measurements were accurate while, in fact, they were biased.
With Björn Hagströmer, I have worked for years trying to prove that there is such bending bias in measurements of information shares in microstructure research. The reason is the following. Consider the simplest case where a researcher has access to a sample of transaction prices and midquotes, where the latter is the average of the best bid and ask.
Oftentimes, one is interested in learning how informative quotes and trades are on the fundamental value of the security. Do they both contribute 50%? Or, are quotes more informative than trades? And, if so, by how much? Consider the following snapshot of quotes and trades.
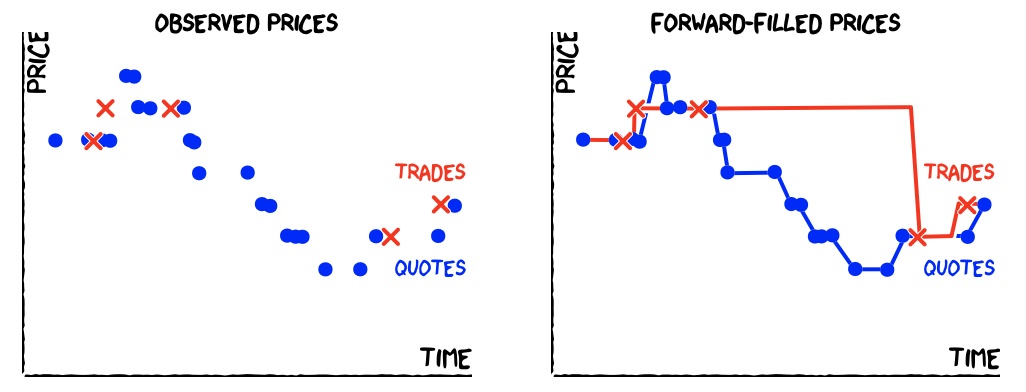
The de facto standard approach forward-fills prices and estimates information shares that way (Hasbrouck, 1995). We believe that such forward-filling is not as innocent as it may sound. The forward-filling of quotes makes economic sense, as quotes remain available for trade, until changed. Forward-filling trade prices, however, does not, since trades reflect a deal at a specific point in time. In sum, quotes should be considered as a continuous time series, whereas trades are an event time series.
The reason that forward-filling is not innocent can be seen in the above snapshot. Mechanically forward-filling and estimating information shares disadvantages trade prices. Note how, in the period between the third and fourth trade, the price seems to move towards the quote series, and away from the (stale) trade price series. In our view, this period should be parsed as trade prices simply not being available. Forward-filling thus constitutes a bending force towards quotes, and away from trades.
In the paper we released today, we show that, indeed, forward-filling can bias information estimates in favor of quotes. We do so through simulations from a model that is calibrated to real-world data. With the insights we obtain in the lab, we propose an alternative approach that yields unbiased information share estimates. In a nutshell, our approach avoids the forward-filling of trade prices by using signed volume instead of trade prices. This way of analyzing the information in trades had been proposed in Hasbrouck (1991).
Our approach, therefore, effectively marries Hasbrouck (1991) with Hasbrouck (1995) to create an approach that can handle modern hybrid markets, where securities trade not only on many exchanges, but also in different types of off-exchange venues. Modern datasets therefore consist of many series of quotes and trades for the same security. Our approach yields unbiased information shares for all of these.
In one of my daydreams, a picture of Björn and myself, along with many of you, will become a classic.
;-).