

The VIX is often referred to as the fear gauge. But, what exactly do investors fear?
My conjecture is that it is the fear of forced selling. I propose a Grossman-Stiglitz type model to show that, indeed, VIX could be a gauge of fire sales.
The Volatility Index (VIX) was launched in 1993 by the Chicago Board Options Exchange (CBOE). The CBOE refers to it as an “index to measure the market’s expectation of future volatility.”1 This is, at best, only partially true. If one compares the realized variance of S&P500 index returns to the variance implied by the VIX over the lifetime of the VIX, then the latter is 31% higher.
| Variance type | Average 1993-2024 |
|---|---|
| Realized variance S&P 500 return (%, annualized) | 342 |
| Implied variance (VIX squared) | 447 |
| Difference | +31% |
This wedge between implied and realized variance is well known in the academic literature. It is referred to as the variance risk premium (VRP). It has been documented to be positive on average. And, it is significantly higher in the months after a crisis.
A positive VRP has been explained with time-varying volatility,2 but a rational explanation for an elevated VRP in the months after a crisis remains elusive.3
I have long had the intuition that the key to understand these puzzling findings might lie in trading the index. I analyzed SPY, which is arguably the largest exchange traded fund (ETF) that tracks the S&P 500 index. It was launched in 1993 and, therefore, intraday trade data is available since the inception of VIX in 1993. Simple averaging across crisis periods show that:
The model expands the Grossman-Stiglitz type model proposed by Vayanos and Wang (2012, RFS). Information is symmetric across agents in their baseline version. I add a variance swap to this version of the model in order to price its payoff, i.e., being paid realized variance. The late Peter Carr eloquently argued that the price of such swap is approximately equal to VIX squared. Solving the model, therefore, yields an equilibrium expression for VIX. In closed form.
The model consists of three periods. Agents are identical initially, then become heterogeneous due to nontraded risk shocks which trigger trade, and, finally, they consume their payoffs. The engine of all results is the second period, in which the agents who experience the shock, become liquidity demanders to hedge the shock. The correlation of the shock is such that demanders need to sell in bear markets and buy in bull markets. This pattern could be interpreted as leverage-induced trading.
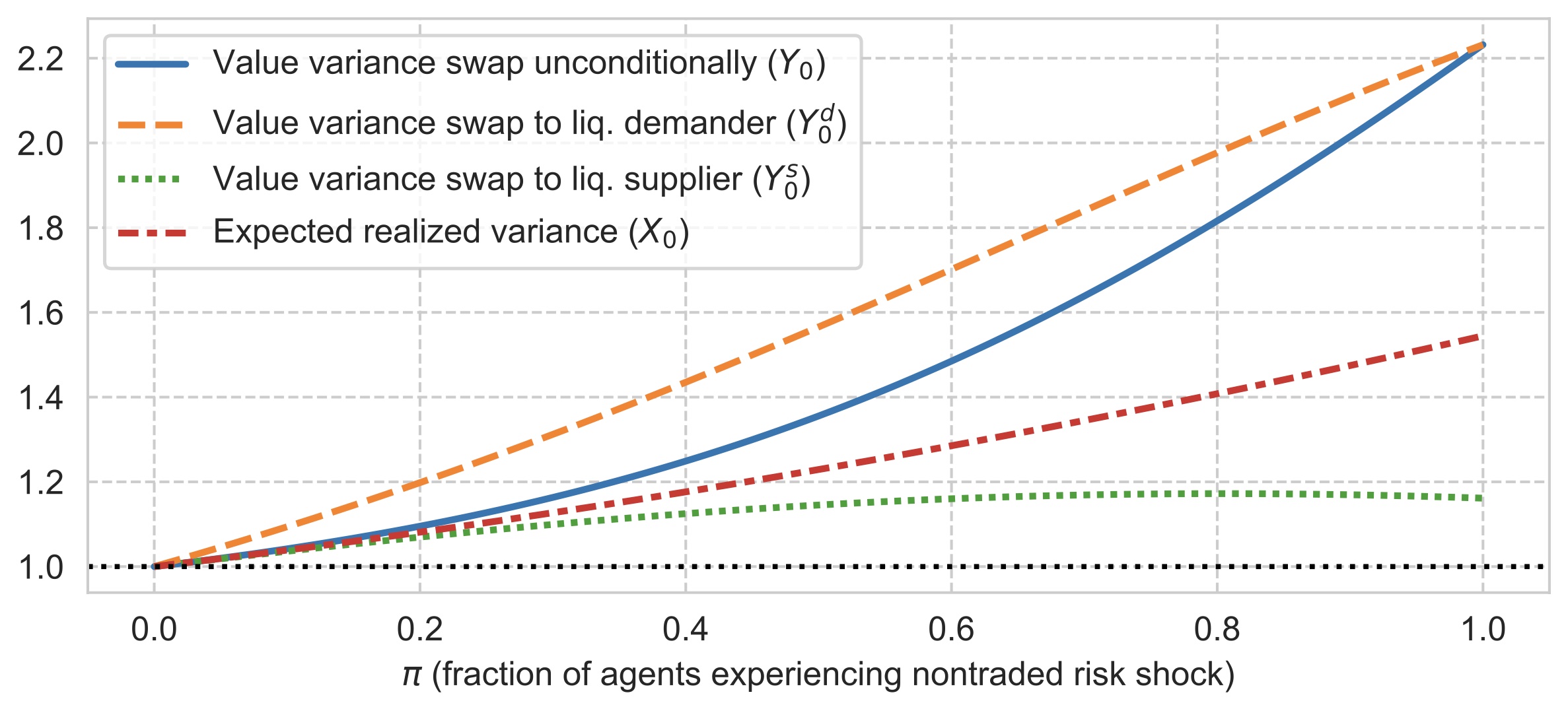
The figure above is the signature graph of the paper. It shows how the value of the variance swap, i.e., VIX squared, depends on the fraction of agents who experience the shock in period two. The blue solid line shows that this value monotonically increases in the fraction of shocked agents. It is a probability weighted sum of the value attached to the swap by shocked agents who become liquidity demanders, and the others who endogenously become liquidity suppliers. Demanders value the swap higher than expected realized variance. Suppliers value it lower.
Note that this expected realized variance itself increases in the fraction of shocked agents. This is due to (transitory) price pressures that are needed to clear the market. They compensate liquidity suppliers for taking on more risk. These pressures add to realized variance and, therefore, to the payoff of the variance swap.
Importantly, the model findings can explain the empirical patterns:
An extremely short summary of the rich set of results that the model yields is: VIX is an index to measure (investor) utility cost of fire sales. One might say that the model puts flesh and bones on the popular saying that VIX is …
… a fear gauge.
Please find the paper here.
See, for example, Bollerslev, Tauchen, and Zhou (2009, RFS) or Todorov (2010, RFS). ↩︎
Lochstoer and Muir (2022, JF) propose an explanation based on agents who update too slowly to changing volatility. ↩︎