

Estimates are inherently uncertain. In the late 1800s, the British statistician Udny Yule coined the term standard error to refer to such uncertainty. In 1897, he wrote:
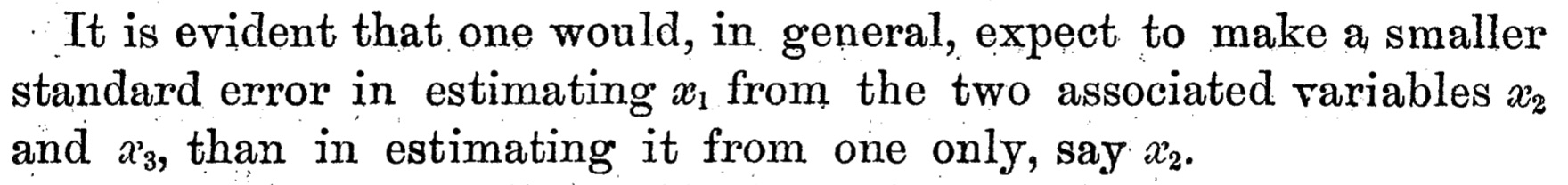
He essentially says that with each additional data point, the uncertainty in an estimate declines. The standard error becomes smaller. Larger samples make for better estimates.
Does this mean that in an era of Big Data we estimate with great precision? Yes, provided we agree on how to measure what we are interested in. Yule’s statement in the banner to this blog post, however, hints at another level of uncertainty:
We frequently measure that which we can rather than that which we wish to measure… and forget that there is a difference.
He argues that there is room between what we wish to measure and what we can measure. In other words, if two research teams were given the same “wish,” then their results might differ if this target is beyond reach. They will have to take inventory of all that can be measured, and pick a preferred one.
It is, however, unlikely that the two teams would pick the same measure. The result will therefore likely differ across the two teams. Suppose only one team were tasked with measurement, then does all of the above not imply that this adds a layer of uncertainty to the result it reports?
How large is this additional layer of uncertainty? Since it is due to the lack of a standard (measure), one could say how large is the nonstandard error?
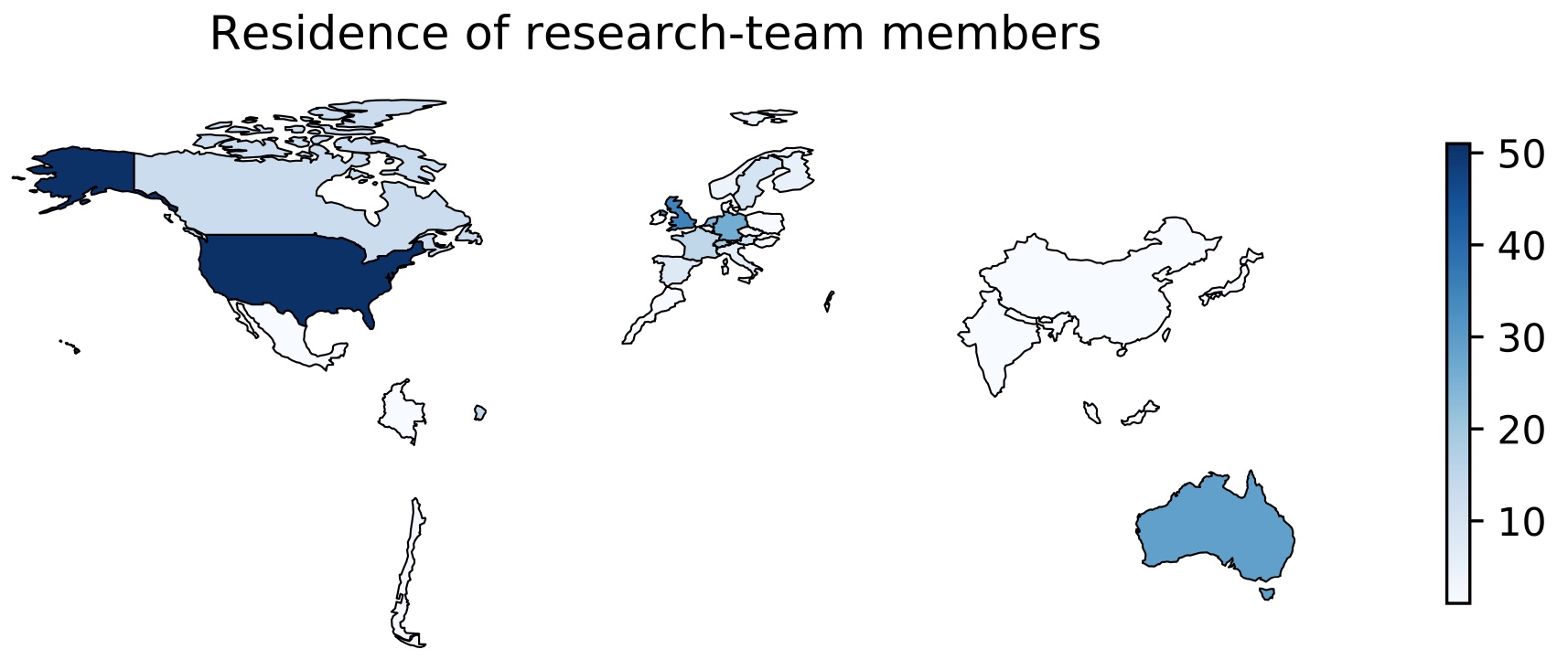
In an attempt to measure the size of nonstandard errors, we let 164 research teams independently test the same six hypotheses on the same data. We believe that the teams are well qualified for the tasks. They signed up from all over the globe as the map below shows.
Long story short: Last week we released the results of the project. We find that nonstandard errors are surprisingly large, even for a sub-sample of “highest quality results.” In the project, nonstandard errors are similar in magnitude as the (mean) standard error.
There is lots more to say, but I like to conclude by sharing one more finding. In the project, the teams were asked, ex-ante, to assess the size of the (realized) nonstandard error. They vastly underestimated it, thus adding some truth to Yule’s conjecture:
…and forget that there is a difference.